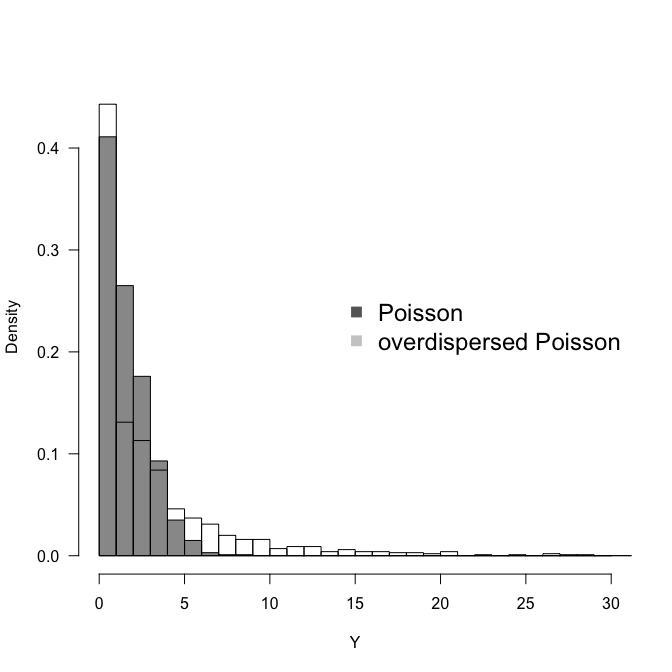
Overdispersion

In statistics, overdispersion is the presence of greater variability (statistical dispersion) in a data set than would be expected based on a given statistical model. Overdispersion is often encountered when fitting very simple parametric models, such as those based on the Poisson distribution and this will usually lead to inflated Type I error rates. The Poisson distribution has one free parameter and does not allow for the variance to be adjusted independently of the mean. The choice of a distribution from the Poisson family is often dictated by the nature of the empirical data. For example, Poisson regression analysis is commonly used to model count data. If overdispersion is a feature, an alternative model with additional free parameters may provide a better fit. In the case of count data, a Poisson mixture model like the negative binomial distribution can be proposed instead, in which the mean of the Poisson distribution can itself be thought of as a random variable drawn – in this case – from the gamma distribution thereby introducing an additional free parameter (note the resulting negative binomial distribution is completely characterized by two parameters).

Example: Extramarital Affairs

Description: Data set includes various social and marital factors along with the count of extramarital affairs for 600 people.

naffairs: Number of affairs within last year.
kids: 1=have children 0=no children.
vryunhap: Very unhappily married (1/0).
unhap: Unhappily married (1/0).
avgmarr: Average married (1/0).
hapavg: Happily married (1.0).
vryhap: Very happily married (1/0).
antirel: Anti-religious (1/0)
notrel: Not religious (1/0).
slghtrel: Slightly religious (1/0).
smerel: Somewhat religious (1/0).
vryrel: Very religious (1/0).
yrsmarr1: Year of marriage > 0.75 yrs (1/0).
yrsmarr2: Year of marriage > 1.5 yrs (1/0).
yrsmarr3: Year of marriage > 4.0 yrs (1/0).
yrsmarr4: Year of marriage > 7.0 yrs (1/0).
yrsmarr5: Year of marriage > 10.0 yrs (1/0).
yrsmarr6: Year of marriage > 15.0 yrs (1/0).

Source: https://vincentarelbundock.github.io/Rdatasets/doc/COUNT/affairs.html
Download the data from here

Task: Design a model for estimating number of affairs.

Let's try PROC GENMOD with poisson distribution option:

PROC GENMOD DATA=tutorial.affairs;
CLASS kids--yrsmarr6;
MODEL naffairs = kids--yrsmarr6 / DIST=POISSON;
RUN;
Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF
Deviance 586 2303.1626 3.9303
Scaled Deviance 586 2303.1626 3.9303
Pearson Chi-Square 586 4050.5305 6.9122
Scaled Pearson X2 586 4050.5305 6.9122
Log Likelihood   -235.1784  
Full Log Likelihood   -1398.5763  
AIC (smaller is better)   2827.1525  
AICC (smaller is better)   2827.9730  
BIC (smaller is better)   2893.1314  

‘Criteria For Assessing Goodness Of Fit’ section of output suggests that, because value/df for both deviance and Pearson Chi-Square statistics is much higher than 1, Poisson model is not quite adequate to describe the counts of hypotensions and crampings. It also suggests that there is overdispersion.

Negative-binomial distribution is a benchmark model to account for overdisperion on count responses. We can test for overdispersion in a Poisson model by using the DIST=NEGBIN, SCALE=0, and NOSCALE options in the MODEL statement of PROC GENMOD. When used together, these options test whether overdispersion of the form μ+kμ2 exists by testing whether the negative binomial dispersion parameter, k, is zero. When k=0, the negative binomial distribution is equivalent to the Poisson distribution. Let's test whether there is overdispersion in our data.

PROC GENMOD DATA=tutorial.affairs;
CLASS kids--yrsmarr6;
MODEL naffairs = kids--yrsmarr6 / DIST=NEGBIN SCALE=0 NOSCALE;
RUN;
Lagrange Multiplier Statistics
Parameter Chi-Square Pr > ChiSq  
Dispersion 259.7461 <.0001 *
* One-sided p-value

Our suspicions were correct; there is overdispersion. There are various distributions to implement instead of Poisson:

  • Negative binomial
  • Zero-inflated poisson
  • Zero-inflated negative binomial
  • Hurdle poisson
  • Hurdle negative binomial
  • Generalized poisson
Another option is account for overdispersion with respect to the Poisson model by introducing a dispersion parameter φ into the relationship between the variance and the mean. For example, the code below uses deviance to account for overdispersion.

PROC GENMOD DATA=tutorial.affairs;
CLASS kids--yrsmarr6;
MODEL naffairs = kids--yrsmarr6 / DIST=POISSON DSCALE;
RUN;
Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF
Deviance 586 2303.1626 3.9303
Scaled Deviance 586 586.000 1.000
Pearson Chi-Square 586 4050.5305 6.9122
Scaled Pearson X2 586 1030.5876 1.7587
Log Likelihood   -59.8371  
Full Log Likelihood   -1398.5763  
AIC (smaller is better)   2827.1525  
AICC (smaller is better)   2827.9730  
BIC (smaller is better)   2893.1314  

Scaled Pearson X2 is still well above 1, therefore we will try negative binomial distribution next:

PROC GENMOD DATA=tutorial.affairs;
CLASS kids--yrsmarr6;
MODEL naffairs = kids--yrsmarr6 / DIST=NEGBIN;
RUN;
Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF
Deviance 586 339.8629 0.5800
Scaled Deviance 586 339.8629 0.5800
Pearson Chi-Square 586 566.8541 0.9673
Scaled Pearson X2 586 566.8541 0.9673
Log Likelihood   439.3546  
Full Log Likelihood   -724.0433  
AIC (smaller is better)   1480.0865  
AICC (smaller is better)   1481.0180  
BIC (smaller is better)   1550.4640  

Parameter estimates (not shown) tells us that only unhap, antirel, notrel, slghtrel, yrsmarr1, yrsmarr2, yrsmarr3 are significant. We run our model with only these variables:

PROC GENMOD DATA=tutorial.affairs;
CLASS kids--yrsmarr6;
MODEL naffairs = unhap antirel notrel slghtrel yrsmarr1 yrsmarr2 yrsmarr3 / DIST=NEGBIN;
RUN;
Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF
Deviance 593 338.5604 0.5709
Scaled Deviance 593 338.5604 0.5709
Pearson Chi-Square 593 530.2979 0.8943
Scaled Pearson X2 593 530.2979 0.8943
Log Likelihood   435.7320  
Full Log Likelihood   -727.6659  
AIC (smaller is better)   1473.3317  
AICC (smaller is better)   1473.6363  
BIC (smaller is better)   1512.9191  
Algorithm converged.
Analysis Of Maximum Likelihood Parameter Estimates
Parameter   DF Estimate Standard
Error		 Wald 95% Confidence Limits Wald Chi-Square Pr > ChiSq
Intercept   1 0.6383 0.9363 -1.1968 2.4735 0.46 0.4954
unhap 0 1 -1.0441 0.3624 -1.7544 -0.3339 8.30 0.0040
antirel 0 1 -1.3962 0.4489 -2.2760 -0.5164 9.67 0.0019
notrel 0 1 -1.1257 0.3141 -1.7413 -0.5101 12.85 0.0003
slghtrel 0 1 -1.2156 0.3302 -1.8629 -0.5683 13.55 0.0002
yrsmarr1 0 1 1.3507 0.4769 0.4160 2.2853 8.02 0.0046
yrsmarr2 0 1 1.6580 0.3850 0.9034 2.4126 18.54 <.0001
yrsmarr3 0 1 0.8858 0.3404 0.2187 1.5529 6.77 0.0093
Dispersion   1 7.0132 0.7824 5.6358 8.7272    

Let's also use SAS graphics to see some of the effects of these parameters. Prior to this we need to reformat the data set and create new columns:

DATA DATA=tutorial.affairs;
SET tutorial.affairs;

IF vryunhap = 1 THEN happiness = 'Very unhappy';
ELSE IF unhap = 1 THEN happiness = 'Unhappy';
ELSE IF hapavg = 1 THEN happiness = 'Happy';
ELSE IF vryhap = 1 THEN happiness = 'Very happy';
ELSE IF avgmarr = 1 THEN happiness = 'Very unhappy';

IF antirel = 1 THEN religiosity = 'Anti religious';
ELSE IF notrel = 1 THEN religiosity = 'Not religious';
ELSE IF slghtrel = 1 THEN religiosity = 'Slightly religious';
ELSE IF smerel = 1 THEN religiosity = 'Somewhat religious';
ELSE IF vryrel = 1 THEN religiosity = 'Very religious';

IF yrsmarr1 = 1 THEN years = '0.75';
ELSE IF yrsmarr2 = 1 THEN years = '1.5';
ELSE IF yrsmarr3 = 1 THEN years = '4';
ELSE IF yrsmarr4 = 1 THEN years = '7';
ELSE IF yrsmarr5 = 1 THEN years = '10';
ELSE IF yrsmarr6 = 1 THEN years = '15';

cnt=1;
RUN;

Now let's use a few graphs to understand these variables:

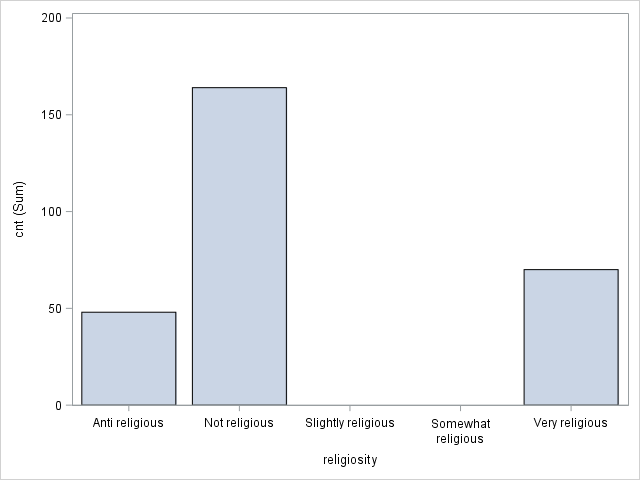
PROC SGPLOT DATA=tutorial.affairs;
VBAR religiosity / RESPONSE=cnt STATSUM;
XAXIS VALUES =('Anti religious' 'Not religious' 'Slightly religious' 'Somewhat religious' 'Very religious');
RUN;

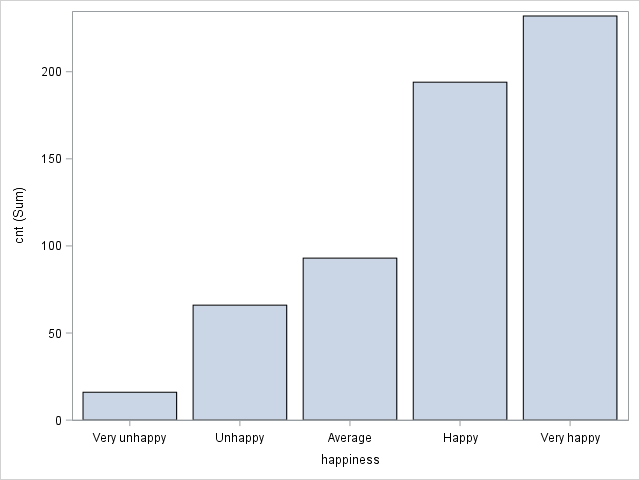
PROC SGPLOT DATA=tutorial.affairs;
VBAR happiness / RESPONSE=cnt STATSUM;
XAXIS VALUES =('Very unhappy' 'Unhappy' 'Average' 'Happy' 'Very happy');
RUN;

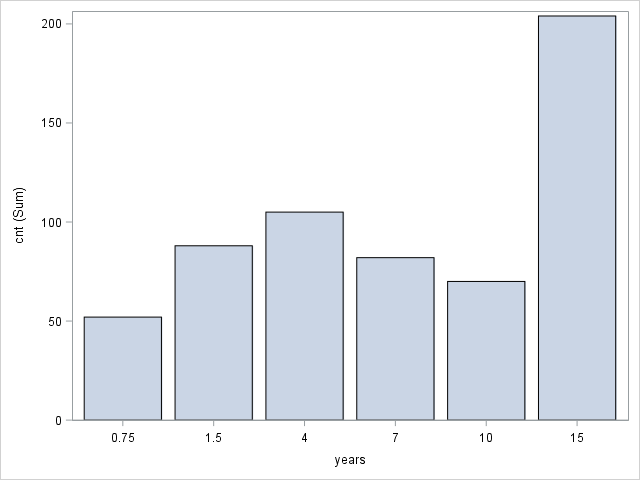
PROC SGPLOT DATA=tutorial.affairs;
VBAR years / RESPONSE=cnt STATSUM;
XAXIS VALUES =('0.75' '1.5' '4' '7' '10' '15');
RUN;