Power and Simple Size Analysis
Sample size determination is an important and often difficult step in planning an empirical study. The cost of studying an entire population is usually prohibitive to both researchers and those being studied in terms of privacy, time, and money. Therefore, a subset of a given population must be selected; this is called sampling. Sampling is a strategy used to select elements from a population. A sample is a subset of the population elements that results from a sampling strategy. Ideally, a sample is selected that is representative of a population (i.e., elements accurately portray characteristics of the population).
Power and sample size analysis optimizes the resource usage and design of a study, improving chances of conclusive results with maximum efficiency. The POWER procedure performs prospective power and sample size analyses for a variety of goals, such as the following:
- determining the sample size required to get a significant result with adequate probability (power)
- characterizing the power of a study to detect a meaningful effect
- conducting what-if analyses to assess sensitivity of the power or required sample size to other factors
Sample Size
Because a sample is only part of a population, generalization from a sample to a population usually involves error. There are two basic types of error that can occur in the process of generalizing from a sample to a population: sampling, or random, error and nonsampling, or systematic, error (SE). The latter type of error also is called bias.
Sampling error results from the 'luck of the draw': too many elements of one kind and not enough elements of another kind. As sample size increases, SE decreases, albeit slowly. If the population is relatively homogeneous, SE will be small.
Nonsampling error is often a more serious problem than SE, because nonsampling error cannot be controlled by increasing sample size. Nonsampling can be organized into three categories:
- Selection bias is the systematic tendency to exclude some elements from the sample. With an availability sample, selection bias is a major concern. In contrast, with a well designed probability sample, selection bias is minimal.
- Nonresponse bias is present to the extent that respondents and nonrespondents differ on variables of interest, and extrapolation from respondents to nonrespondents will be problematic.
- Response bias occurs when respondents ‘shade the truth’ because of interviewer attitudes, the wording of questions, or the juxtaposition of questions.
The size of a sample is an important element in determining the statistical precision with which population values can be estimated. In general, increased sample size is associated with decreased sampling error. The larger the sample, the more likely the results are to represent the population. However, the relationship between sampling error and sample size is not simple or proportional. There are diminishing returns associated with adding elements to a sample.
Example: CD4 Counts for HIV-Positive Patients
Description: CD4 cells are carried in the blood as part of the human immune system. One of the effects of the HIV virus is that these cells die. The count of CD4 cells is used in determining the onset of full-blown AIDS in a patient. In this study of the effectiveness of a new anti-viral drug on HIV, a number of HIV-positive patients will have their CD4 counts recorded and then will be put on a course of treatment with this drug. After using the drug for one year, their CD4 counts will be again recorded. The aim of the experiment was to show that patients taking the drug will increase CD4 counts which is not generally seen in HIV-positive patients. At the end of the study we would like to see, at 95% confidence, between 0.5 and 1 unit difference between control and treatment groups. Expected standard deviation is expected to be between 0.8 and 1.2.
Source: https://vincentarelbundock.github.io/Rdatasets/doc/boot/cd4.html
Download the data from here
Task: Design a balanced study with required number of participants.
We can calculate the number of needed participants with PROC POWER.
PROC POWER;
TWOSAMPLEMEANS
NFRACTIONAL
MEANDIFF = 0.5 TO 1 BY 0.25
STDDEV = 0.8 1.2
GROUPWEIGHTS = 1 | 1
POWER = 0.95
NTOTAL = .;
PLOT x=POWER MIN=0 MAX=1;
RUN;
| Fixed Scenario Elements | |
|---|---|
| Distribution | Normal |
| Method | Exact |
| Group 1 Weight | 1 |
| Group 2 Weight | 1 |
| Nominal Power | 0.95 |
| Number of Sides | 2 |
| Null Difference | 0 |
| Alpha | 0.05 |
| Computed Ceiling N Total | |||||
|---|---|---|---|---|---|
| Index | Mean Diff | Std Dev | Fractional N Total | Actual Power | Ceiling N Total |
| 1 | 0.50 | 0.8 | 135.017481 | 0.951 | 136 |
| 2 | 0.50 | 1.2 | 301.332590 | 0.950 | 302 |
| 3 | 0.75 | 0.8 | 61.130456 | 0.953 | 62 |
| 4 | 0.75 | 1.2 | 135.017481 | 0.951 | 136 |
| 5 | 1.00 | 0.8 | 35.309723 | 0.954 | 36 |
| 6 | 1.00 | 1.2 | 76.825133 | 0.950 | 77 |
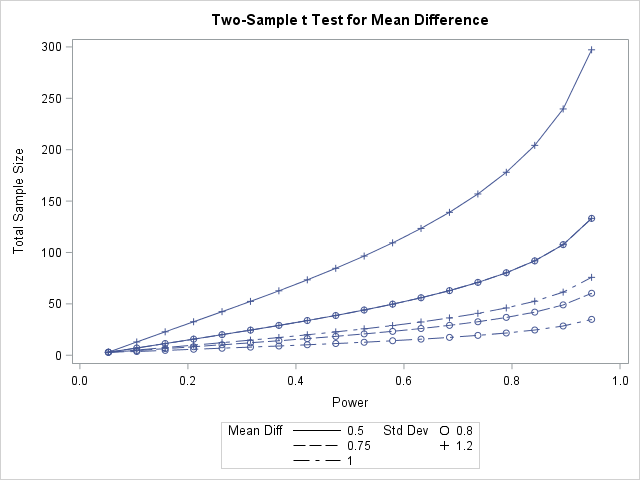
Results show that we wil need a number of participants between 36 and 302. Note how we input the NTOTAL=. Putting a dot in NTOTAL tells SAS to calculate the sample size. We could instead specify the sample size and put a dot in front of POWER= option if we wanted to calculate the power.
- Determining Sample Size: Balancing Power, Precision, and Practicality, P. Dattalo







Leave a Comment