Chi-Sq Test with R

chisq.test in base R package is the tool to use for Chi-Sq tests.

We are going to use the marbles dataset; you can download it from here.

A chi-squared test, also written as χ2 test, is any statistical hypothesis test where the sampling distribution of the test statistic is a chi-squared distribution when the null hypothesis is true. Without other qualification, 'chi-squared test' often is used as short for Pearson's chi-squared test. The chi-squared test is used to determine whether there is a significant difference between the expected frequencies and the observed frequencies in one or more categories.

For example, let's test the assumption that total number of marbles for each color is the same, i.e. P(red) = P(green) = P(blue) = 1/3. To do this we use p argument.

First we need to get the summary data:

# A tibble: 3 x 2
  Color     n
1 blue     24
2 green    21
3 red      15

Now we are ready to use chisq.test

	Chi-squared test for given probabilities
X-squared = 1.8717, df = 2, p-value = 0.3923

Since our p-value = 0.3022 is bigger than 0.05, our equal probability estimation is close but not perfect. Now let's test P(blue) = 0.4, P(green) = 0.35, P(red) = 0.25:

	Chi-squared test for given probabilities
X-squared = 0, df = 2, p-value = 1

What if we want to test whether two bags are identical in terms of color distribution? To test this, we first need to change the shape of the dataframe:

  blue green red
1    8    14   8
2   16     7   7

Now the chisq-test:

	Pearson's Chi-squared test
X-squared = 5.0667, df = 2, p-value = 0.07939

A better example for Chi-Sq test would be to determine relationship between two variables. Let's say we want to analyze the relationship between traffic warning signs and speeding. You can see the data set explanation here. I created a lighter version of the data in R format is here. There are two columns:

• sign: yes or no
• speeding: yes or no

Let's run the test:

	Pearson's Chi-squared test with Yates' continuity correction
X-squared = 148.66, df = 1, p-value < 2.2e-16

p-value for Chi-Sq is less than 0.05 therefore we can conclude that warning signs have an effect on speeding. Note that we have a relatively large sample size therfore Fisher's Exact Test is not needed.

Relative Risk

In medical setting, 2x2 tables are constructed where one variable represents presence/absence of a disease and the other is some risk factor. These studies measures odds ratio by retroactive analysis. If subjects are selected by risk factor and watched over for disease then it is called relative risk (vs odds ratio). In both cases, a risk measure of 1 means no risk. If outcome is a disease, >1 means exposure harmful and <1 means beneficial. Let's have an example.

Our example data is from SAS website and you can download a copy of it from here.

Exposure	Response	Count
0	0	6
0	1	2
1	0	4
1	1	11

 

The data setcontains hypothetical data for a case-control study of high fat diet and the risk of coronary heart disease. The data are recorded as cell counts, where the variable Count contains the frequencies for each exposure (1=high cholesterol diet 0=low cholesterol diet) and response (1=disease 0=no disease) combination.

First we need to convert our dataframe to a 2x2 matrix for further analysis.

Relative Risk calculations are done through epitools package:

Now the calculation:

$data
          HeartDisease
Diet       No Yes Total
  LowChol   6   2     8
  HighChol  4  11    15
  Total    10  13    23

$measure
          risk ratio with 95% C.I.
Diet       estimate     lower    upper
  LowChol  1.000000        NA       NA
  HighChol 2.933333 0.8502063 10.12042

$p.value
          two-sided
Diet       midp.exact fisher.exact chi.square
  LowChol          NA           NA         NA
  HighChol 0.03995399   0.03930542 0.02594405

Relative Risk column shows that high cholesterol diet is at least 11% riskier than low cholesterol diet.

Inter-Rater Reliability

Many situations in the healthcare industry rely on multiple people to collect research or clinical laboratory data. The question of consistency, or agreement among the individuals collecting data immediately arises due to the variability among human observers. Well-designed research studies must therefore include procedures that measure agreement among the various data collectors. Study designs typically involve training the data collectors, and measuring the extent to which they record the same scores for the same phenomena. Perfect agreement is seldom achieved, and confidence in study results is partly a function of the amount of disagreement, or error introduced into the study from inconsistency among the data collectors. The extent of agreement among data collectors is called, “interrater reliability”.

A final concern related to rater reliability was introduced by Jacob Cohen, a prominent statistician who developed the key statistic for measurement of interrater reliability, Cohen’s kappa (5), in the 1960s. Cohen pointed out that there is likely to be some level of agreement among data collectors when they do not know the correct answer but are merely guessing. He hypothesized that a certain number of the guesses would be congruent, and that reliability statistics should account for that random agreement. He developed the kappa statistic as a tool to control for that random agreement factor.

Below is a fictitious data of two raters, Mark and Susan, rating same events. There are agreements (same score) between raters and there are also disagreements (different score) over same events. You can download this data set from here.

Var#	Raters
	Mark	Susan
1	1	1
2	1	0
3	1	1
4	0	1
5	1	1
6	0	0
7	1	1
8	1	1
9	0	0
10	1	1

 

Let's calculate inter-rater reliability statistics of above data with kappa2 function of irr.

 Cohen's Kappa for 2 Raters (Weights: unweighted)

 Subjects = 10 
   Raters = 2 
    Kappa = 0.524 

        z = 1.66 
  p-value = 0.0976 

A Kappa value higher than 0.61 typically indicates strong agreement between raters and anything less than 0.20 means poor agreement. Here we have a Kappa value of 0.5238, therefore we can conclude that raters agree moderately.

Example: Dates of Coal Mining Disasters

Description: This data frame gives the dates of 191 explosions in coal mines which resulted in 10 or more fatalities. The time span of the data is from March 15, 1851 until March 22 1962.

date: The date of the disaster. The integer part of date gives the year. The day is represented as the fraction of the year that had elapsed on that day.
year: The year of the disaster.
month: The month of the disaster.
day: The day of the disaster.

Source: https://vincentarelbundock.github.io/Rdatasets/doc/boot/coal.html
Download the data from here

Task: Analyze whether disasters happen randomly or there is a monthly pattern.

For this task we can use Chi-Sq test for equal proportions. This test would examine whether disasters occured at similar frequencies for each month or not. Note that we don't normally have to use a statistical test for these kind of cases; usually a simple histogram would suffice to show the pattern. Take a look at the number of disasters per year below for example. It is clear that disaster frequency decreases over time, possibly because of better safety measures.

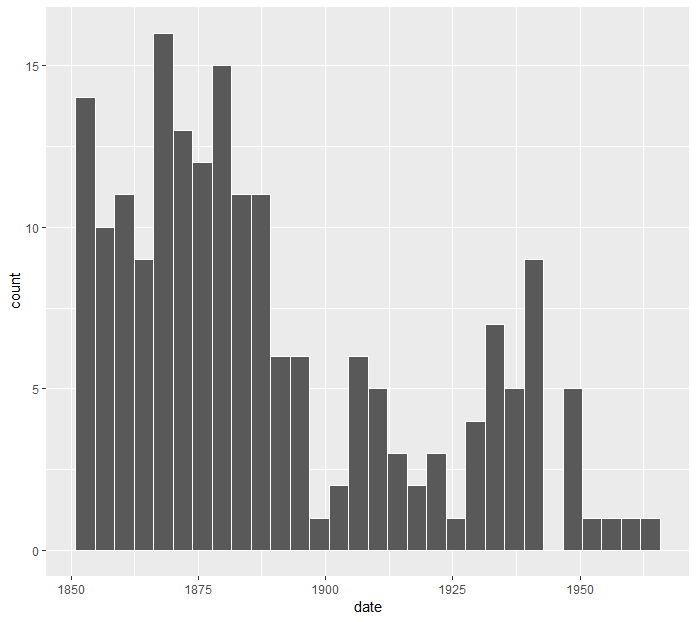
OK, now let's analyze if there is a monthly pattern:

# A tibble: 12 x 2
   month     n
 1     1    14
 2     2    21
 3     3    19
 4     4    12
 5     5    15
 6     6    10
 7     7    17
 8     8    15
 9     9    11
10    10    14
11    11    20
12    12    23

	Chi-squared test for given probabilities
X-squared = 11.743, df = 11, p-value = 0.3832

Let's check the deviation graphically:

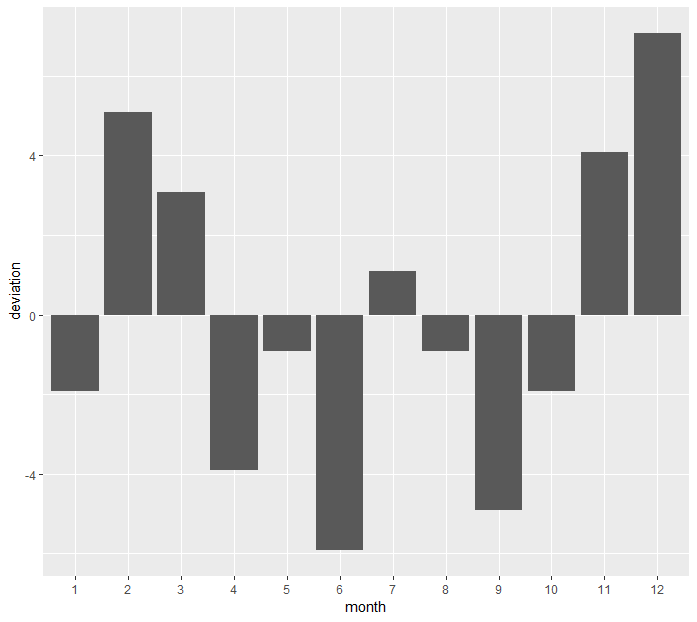
We can see from the deviation graph that disasters tend to happen at colder weather with the exception of January. Also Chi-Sq test tells us that proportions are not equal.